Logic Steps for Annealing (Pseudo-Genetic)
Non-Differential Optimization

Initial Search
Use the User-defined Feasible Domain Bounds. Subdivide each domain of each variable into N subdivisions. Then create an M-dimensional grid of the search space. This will generate N^M search points. It is potentially a time-consuming search, so use as few subdivisions as needed. The minimum subdivisions would be 3, which would only test the Upper, Midpoint, and Lower bound. The number of subdivisions (preferred) should be odd, so as to capture the midpoint in the seach (which should be the most probable best point). The minimum practical subdivision would be 5.

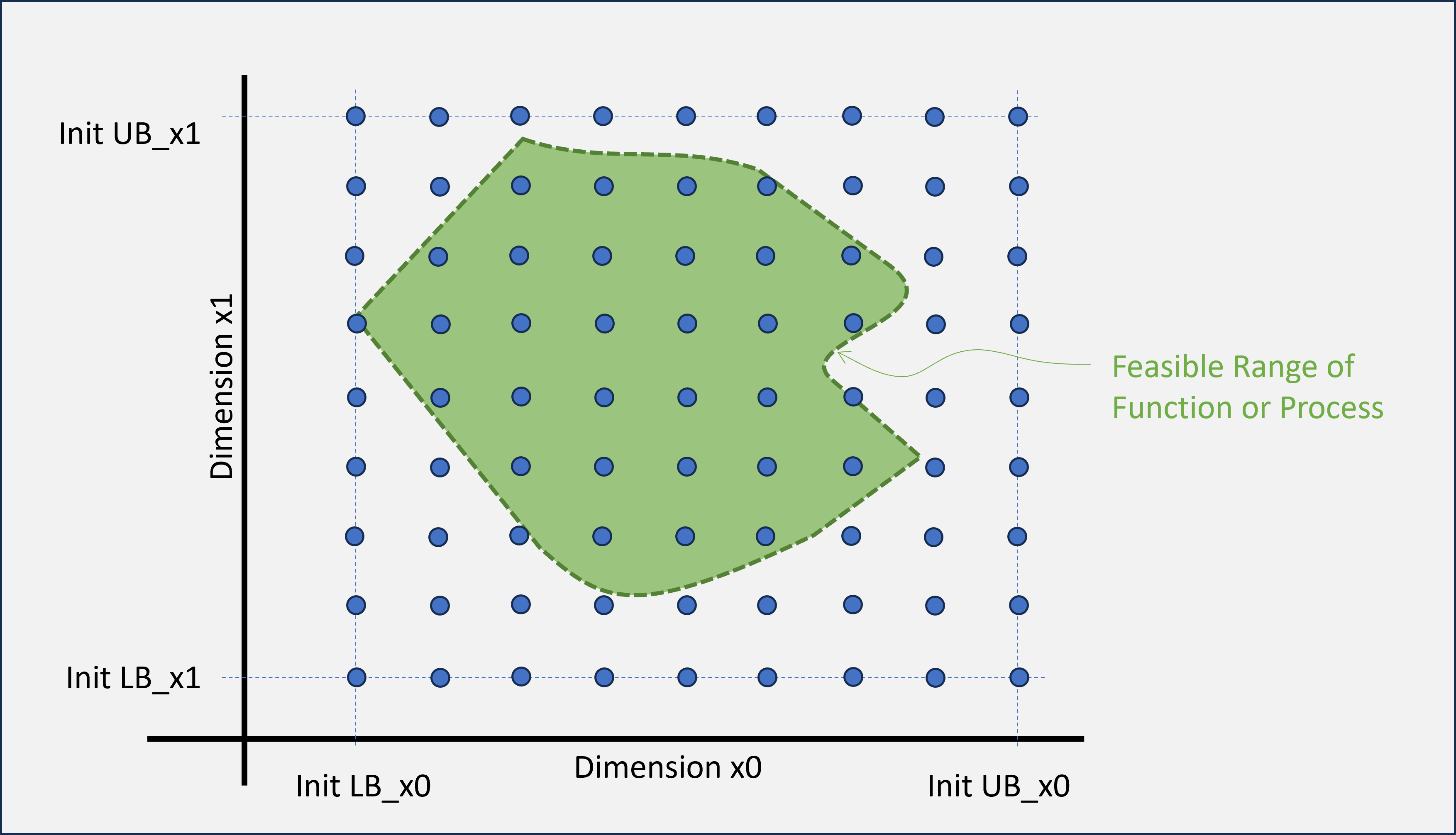
Note: Information on the feasible domain usually not predictable. One benefit of this process, is early detection of invalid portions of the process range. When modeling the Objective Process for Optimization, it is a good idea to generate a special "error" return value; then handle and store these invalid results in a way as to not jeopardize the entire search process.
Sort the Results
The grid of results should be sorted wrt a penalty function. Penalty functions generally do a poor job of identifying the best answer, but with careful consideration, it can trim bad answers effectively. In the sorting process, there are three levels of sorting, not to be done concurrently.
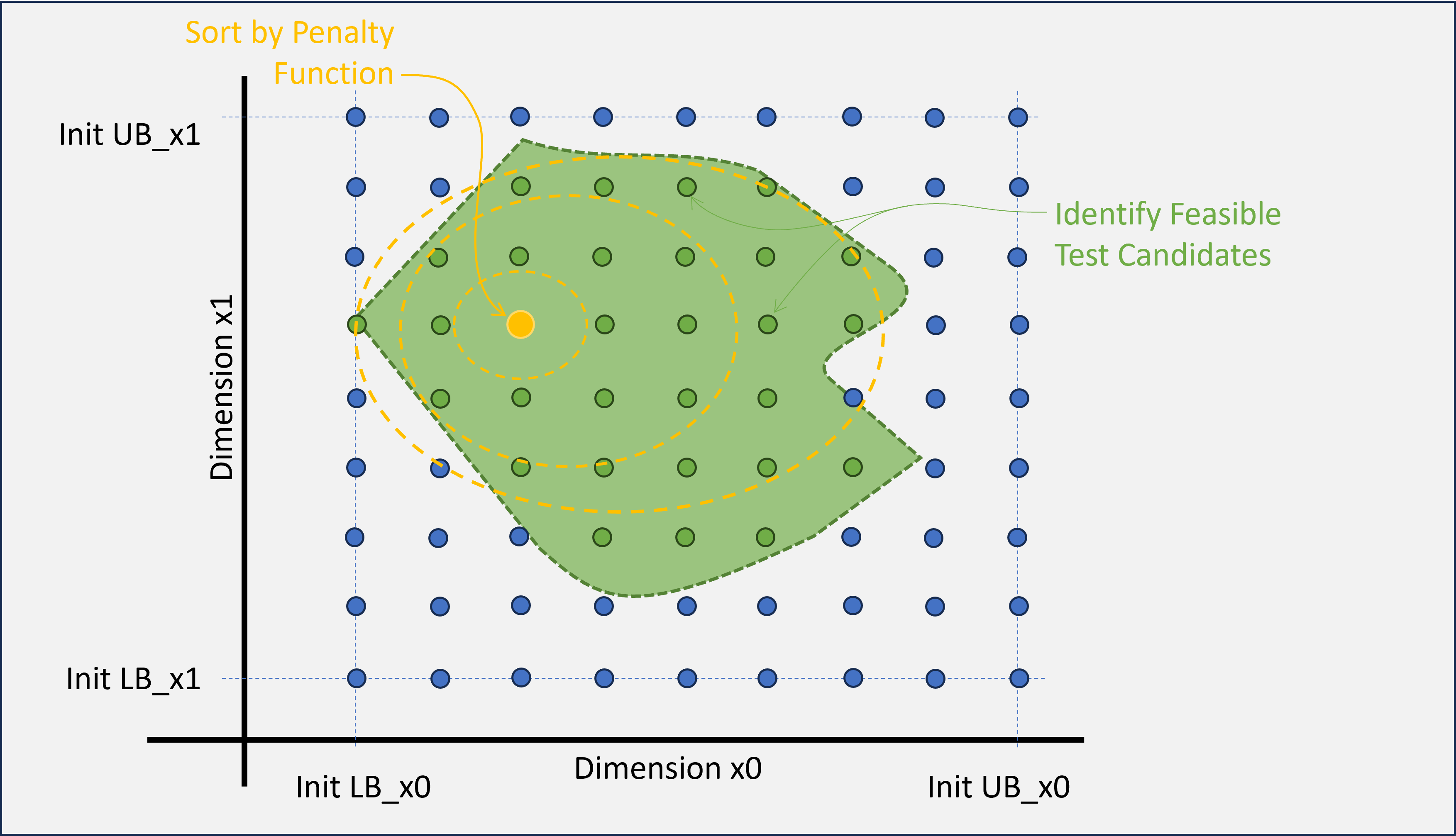
  1. First, do a binary filter of feasible vs. non-feasible; trim infeasible grid points.

  2. Next, sort by the Equality penalty (penalize wrt to compliance to the necessary equality conditions); then trim poor matches.

    Then, sort by the Inequality penalty (penalize wrt compliance to the inequality condition, and do not penalize if the inequality condition(s) is not violated at the grid location); then trim poor matches.

  3. Finally, of the remaining qualified points, sort by the combined penalty function (Objective Function + Penalty); and trim the poor performers (if a statistically-sufficient number of candidates remain).
Shrink the Domain(s)
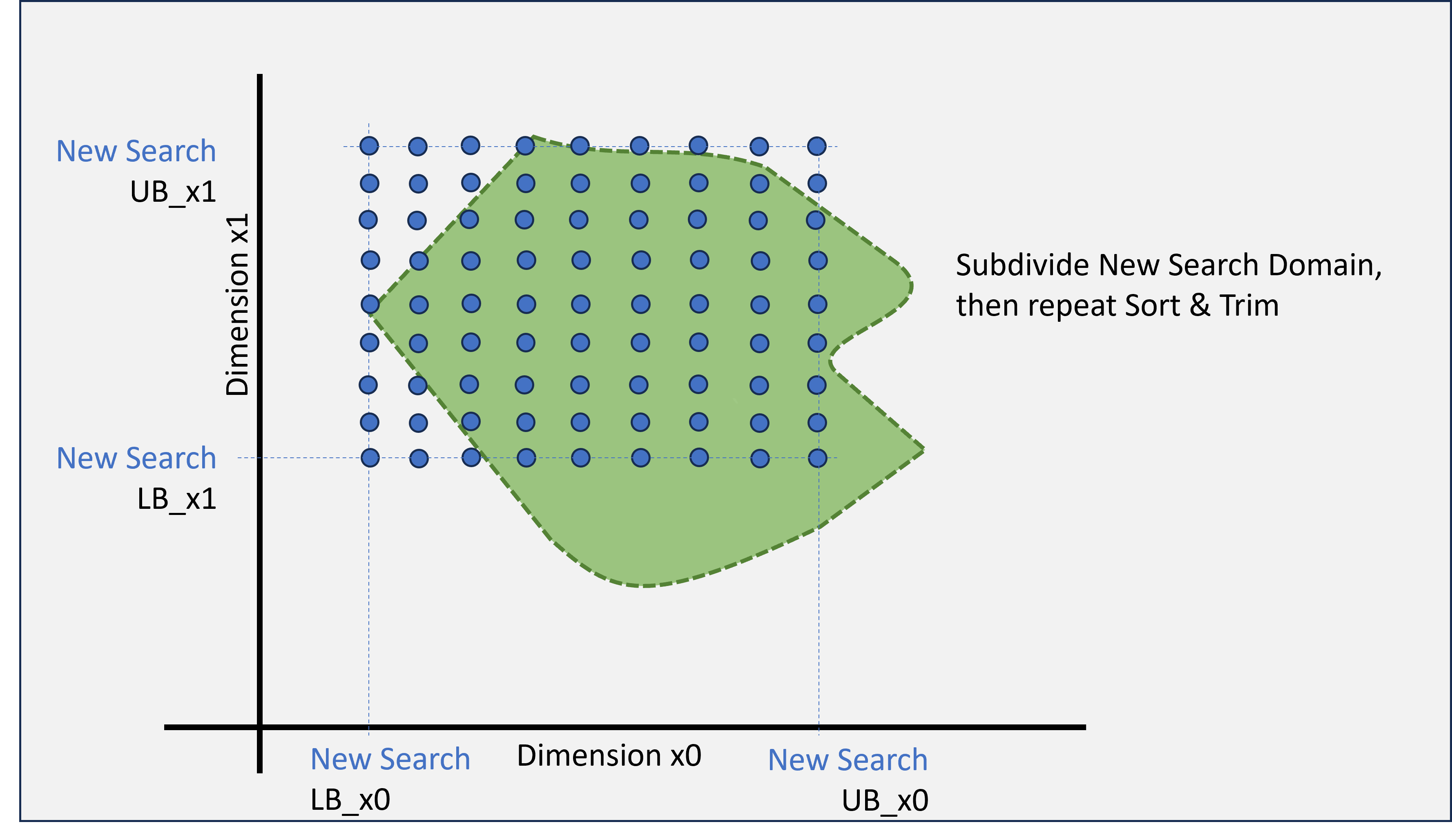
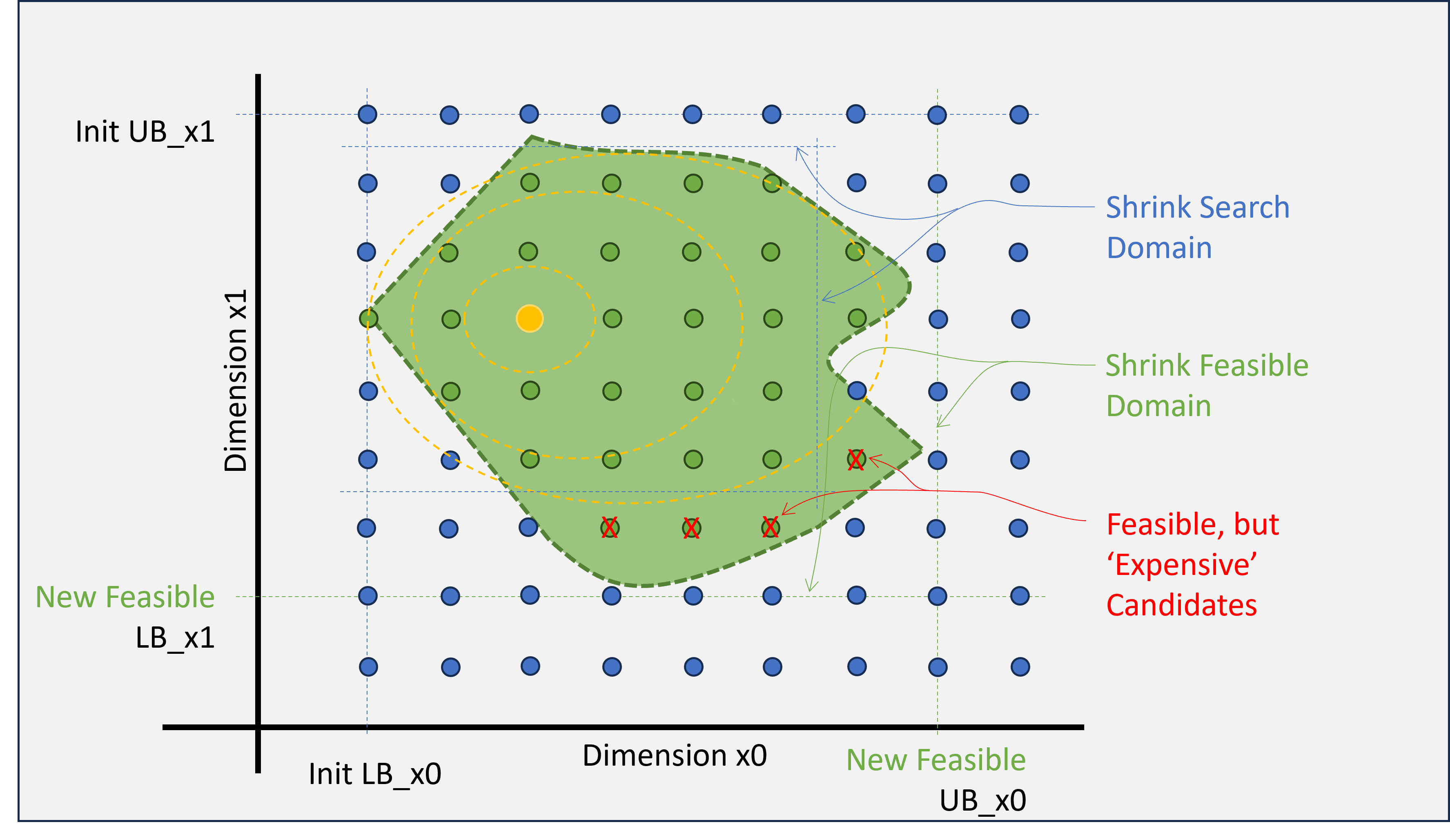
  1. First, (if applicable) trim the overall feasible Bounds. Do not move the boundary any smaller than what you have tested, and any dimension that yields a feasible result wrt any other dimensions should be preserved.

  2. Second, trim the domains with respect to the (feasible) penalty function evaluations. The trimmed domain wrt a given dimension should be the midpoint of the outer most valid and trimmed domain. This would allow for the possibility that a minimum is near an edge, but is still feasible.
Repeat the Search Process
  1. For a general understanding of the problem, this may not be required, or advisable. The pre-process approach will likely provide a good initial search argument.

  2. However, if this Objective Function (or Process) is non-differentiable and/or discontinuous, (or perhaps even for very complex Objective Functions), this entire approach to optimization is a valid search method in its own right. The domains should converge wrt the overall preferred combination of independent variables, and can even generate unexpected results by searching combinations of inputs that may have gone unnoticed, or deemed impractical.